Digital Analytics
Digital Analytics
I have now made two versions of the calculator, 2.02, and 2.51. 2.02 is FREE. 2.51 works like 2.02, if you wish, but also allows units to be attached to the numbers, and does unit conversions as it calculates.
Rather than with very old-style calculators which did only one operation at a time, my calculators evaluate a numerical expression all at once using the standard rules of programming languages. The user can edit the expression--it's just a line of text which can be edited, pasted to or from Notepad, etc. My goal is to produce something that works at least as well as my old TI-30XII electronic device which has been in production a long time and computes a numerical expression. But it is easier to edit with the computer than with the TI-30XII. My calculators obviously do not look like electronic calculators (there is no array of number keys), and they would not fit on an Android screen. But I have come up with 2.5 which appears to be a unique tool for science and engineering.
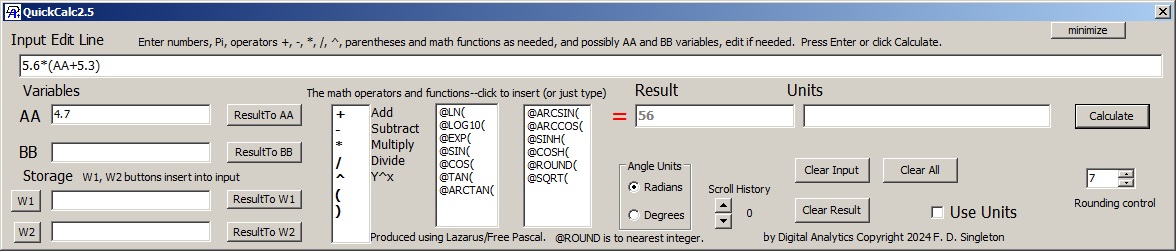
To use either calculator in the most basic way you can type a numerical expression into the input line. When you press the "Enter" key or click on "Calculate" the calculated result appears in the Result box. If you save "Result" into boxes marked AA or BB or type numbers into them, you can input an expression containing variables AA and/or BB and values will be substituted when the computation is done. "Working" text boxes W1 and W2 have been added, which can be inserted into the input line at its blinking caret. Since the input line, AA, BB, W1, and W2 are just text they can be copied and pasted to or from other applications like Notepad.
New for 2.01/2.5 was that every time a calculation is done, it is saved in a memory which can hold the up to the most recent 9 calculations. The AA and BB values for a calculation are saved along with the calculation; W1 and W2 are not. You review previous calculations with the "Scroll History" control (the TI-30XII has something similar).
There is no array of number keys because you can just as well type them on the keyboard, but there are the +,-,*,/,and ^ operators plus ( and ). Clicking on them inserts the operator/parenthesis at the blinking caret (or more easily you can just type them). Also, a set of logarithmic and trigonometric functions are shown in two columns. Clicking inserts them. As in EDTECH they all start with @. @ARCSIN( represents inverse of @SIN(, @ARCCOS( inverse of @COS, etc.
You may freely use floating point notation e.g. 1.34E-3 or 45.3e+03 etc when entering numbers. You can use pi, a number supplied by Free Pascal. The result box may contain either regular decimals or floating point depending on what is appropriate.
You can compute integer powers of negative numbers but with non-integer powers of negatives there is an error.
Version 2.5 lets you turn on a units feature so numbers can be followed by unit abbreviations enclosed in curly brackets. The units are processed during multiplcation, division, or exponentiation calculations within formulas. Simple example--area calculation:
25{m}*5{m} = 125{m^2}
Turning on units also shows tables containing over 80 unit conversion factors which can be inserted into your input formula by clicking, and there are conversion functions for various temperature scales. Conversions are given for length, area, volume, time, energy, force, power, pressure, electrical, density, viscosity, thermal conductivity, specific heat capacity, and temperature. Constants are present in the tables for Avogadro's number, Boltzmann's constant, the gas constant in 3 different sets of units, and the speed of light.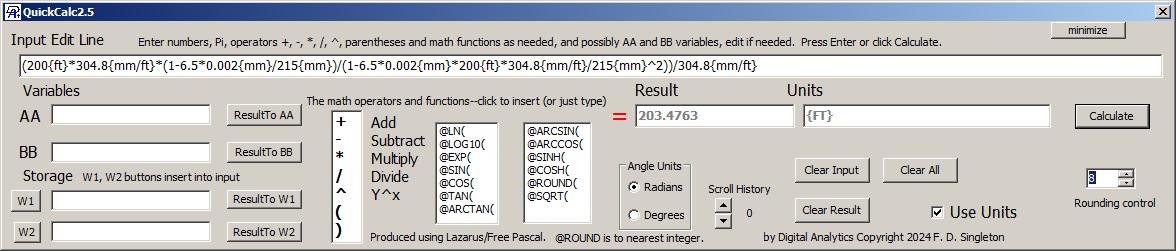
The illustration shows the calculator with a rather large formula. Virtually the same result value was obtained with an Excel formula. Simple unit conversions are present. This is from a study of camera depth-of-field. If the camera is focused exactly on an object 200 ft away, the lens has 215 mm focal length, an f-number (dimensionless) of 6.5, and a focus tolerance of no more than 0.002 mm too far behind the camera's sensor is tolerable, then objects out to 203.5 ft are in range. Note that in 0.002{mm}/215{mm} the units cancel allowing a subtraction of one dimensionless number from another. Attempts to add or subtract numbers with different units produce an error message.
The corresponding opposite case is
(200{ft}*304.8{mm/ft}*(1+6.5*0.002{mm}/215{mm})/(1+6.5*0.002{mm}*200{ft}*304.8{mm/ft}/215{mm}^2))/304.8{mm/ft} = 196.641{FT}
With my camera at its most extreme telephoto setting (215 mm) and the target object at 200 ft, a tolerable depth of focus might be 196.6 ft to 203.5 ft.
For a more complicated unit conversion example the conversion from "customary" to metric units of thermal conductivity is
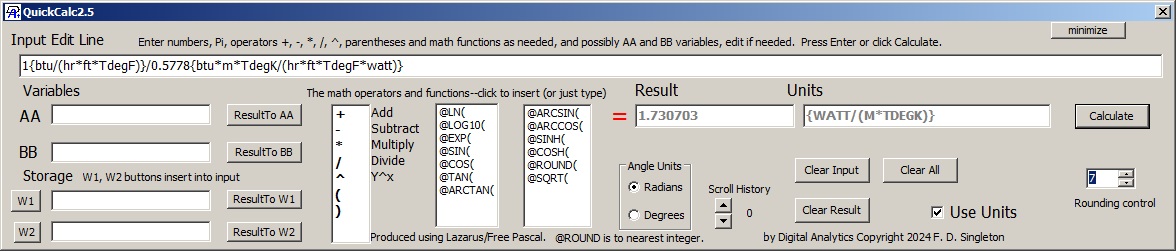
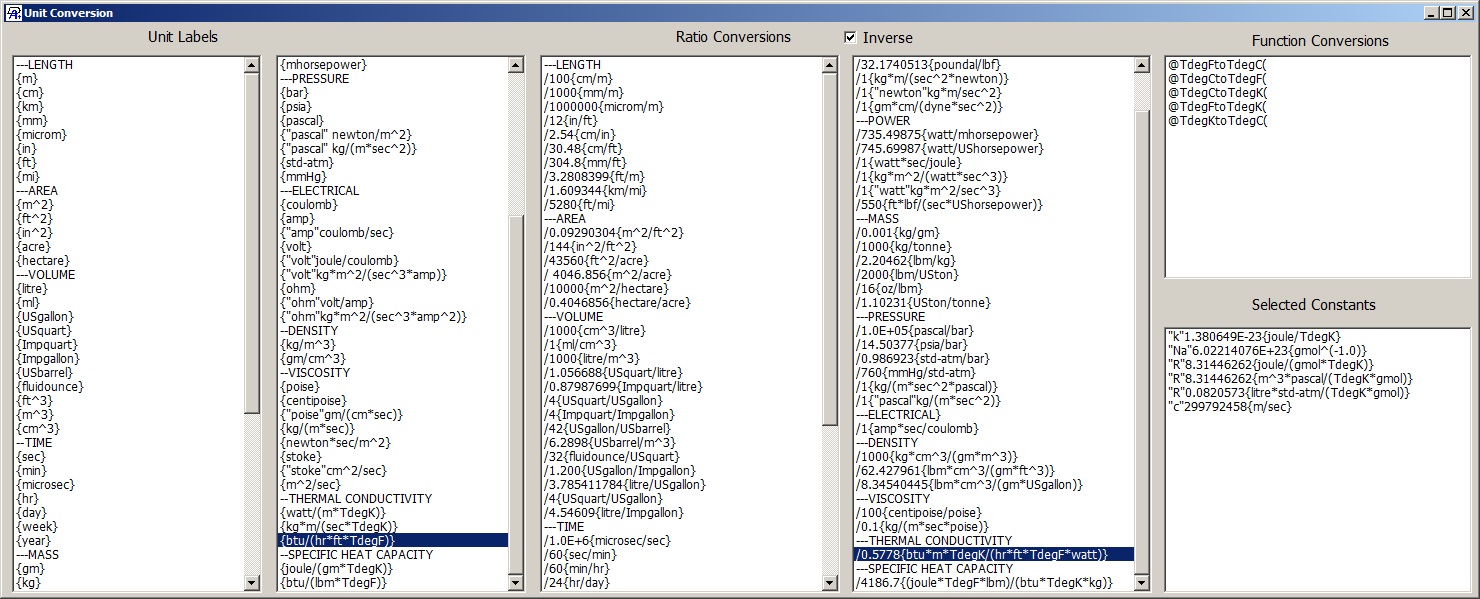
This is created from the clickable unit conversion tables (I only typed the "1" at the beginning). I checked the "inverse" box. I would uncheck it to convert in the opposite direction.